[문제출처 | https://www.acmicpc.net/problem/2775 ]

💭접근 방식
다이나믹 프로그래밍 분류에 있는 문제로, 브론즈 등급이라 큰 어려움은 없었다.
DP 특유의 점화식 규칙 찾기가 어떤 식인지 입문하기 괜찮은 문제였다.
입력으로 들어오는 수의 최대값도 14로 작으니
1. DP용 가구원 수를 담을 배열 선언
2. 규칙을 찾아 전 층의 가구원 수를 DP 배열에 담는다.
3. 테케 별 해당 층, 호의 가구원 수 출력
DP 문제들의 주요 포인트는 점화식과 기저조건을 찾아내는 것이라 생각한다.
자세한 풀이는 아래 풀이 과정에서 풀어보겠다.
📝풀이 과정
변수
- apart[15][14] : 메모이제이션을 위한 2차원 배열. 0 ~ 14층(15행), 1 ~ 14호(14열)
주요 풀이
k층 n호의 가구원 수는 k-1층의 1~n호 가구원 수의 누적합이다.
이때, 입력값은 1 <= k, n <= 14. 아파트는 0층부터 존재하며 각 층에는 1호부터 있다고 했으니
결국 0 ~ 14층, 1 ~ 14호까지 있다는 의미이다.

0층의 입력값은 주어지지 않으니 0층의 가구원 수는 기저조건으로 미리 채울 수 있다.

어떤 규칙이 있는지 간단하게 0 ~ 1층까지만 봐도 쉽게 알아낼 수 있는데 다음 그림과 함께 설명한다.
1층의 각 호의 가구원 수는 1-1층, 즉 0층의 해당 호의 가구원 수 누적합을 갖는다.

1층 1호의 가구원 수는 0층 1호의 가구원 수만큼
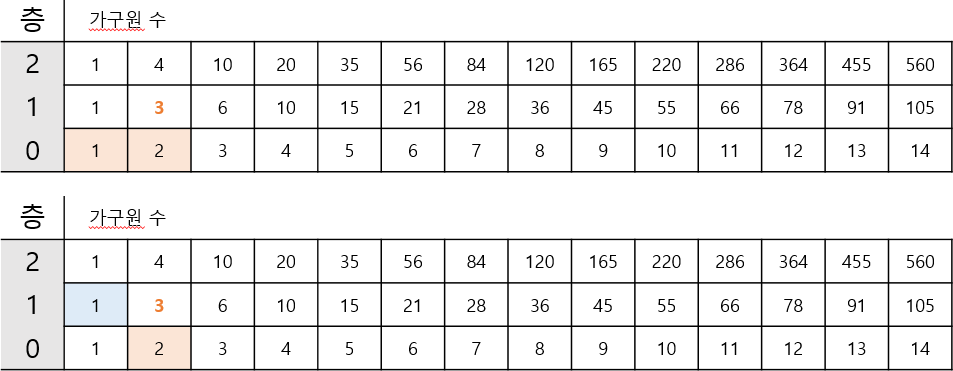
1층 2호의 가구원 수는 0층 1호+2호 가구원 수와 같은데(윗쪽 표) 0층 1호의 값은 1층 1호와 같다.
그렇다면 1층 1호+0층 2호의 값과 같다고 표현할 수 있지 않은가?
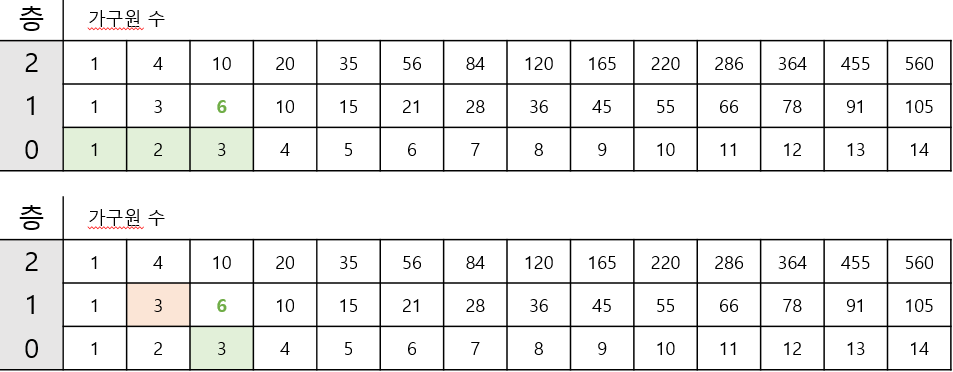
1층 3호의 가구원 수는 0층 1호+2호+3호 가구원 수와 같은데 이 역시 1층 2호가 이미 0층 1호+2호의 합산을 가지고 있다.
즉, 1층 2호(=0층 1호+0층 2호)+0층 3호 값과 같다고 표현할 수 있다.
이쯤 되니 규칙이 보인다.
현재 구해야 하는 k층 n호의 가구원 수는 k층 n-1호 가구원 수 + k-1층 n호 가구원 수다.
단, 어느 층이던 1호는 이전 호가 없기 때문에 k-1층의 1호 가구원 수를 그대로 가져간다.
제한 범위가 작아서 미리 전 층의 가구원 수를 채우고 입력값을 받도록 한다.
위에서 찾은 규칙을 바탕으로 조건과 점화식을 적용한다.
- if(i == 0) { apart[0][j] = j + 1; }: 2차원 배열을 돌며, 0층일 땐 1 ~ 14까지의 값을 저장
- else { apart[i][j] = j > 0 ? apart[i-1][j] + apart[i][j-1] : apart[i-1][j]; } : 0층이 아닐 경우(1층 이상부터)
- 삼항연산자(j > 0 ?) : 0호 이상(문제 상의 1호부터를 배열 인덱스 0으로 표기) 이면
- apart[i-1][j] + apart[i][j-1] : 전 층의 현재 호 + 현재 층의 이전 호 가구원 수
- apart[i-1][j] : 0호일 땐 전 층의 현재 호, 결국 모두 1로 똑같다.
📚참고 자료
이번 문제에서는 없다.
💡정답 코드
결과| 100점, 메모리 14016KB, 시간 100ms
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int apart[][] = new int[15][14]; // 0~14층, 1~14호
for(int i = 0; i < apart.length; i++) {
for(int j = 0; j < apart[i].length; j++) {
if(i == 0) {
apart[0][j] = j + 1;
} else {
apart[i][j] = j > 0 ? apart[i-1][j] + apart[i][j-1] : apart[i-1][j];
}
}
}
int T = Integer.parseInt(br.readLine()); // 테케 수
for(int t = 0; t < T; t++) {
int k = Integer.parseInt(br.readLine()); // 층
int n = Integer.parseInt(br.readLine()); // 호
sb.append(apart[k][n-1]).append("\n");
}
System.out.println(sb.toString());
}
}
'알고리즘 > BAEKJOON' 카테고리의 다른 글
| [BFS] 백준 27737 버섯 농장(서브태스크) JS (1) | 2025.03.08 |
|---|---|
| [DFS] 백준 27737 버섯 농장(서브태스크) JAVA (0) | 2025.03.08 |
| [BFS] 백준 1012 유기농 배추 JAVA (0) | 2022.09.22 |
| [구현] 백준 11558 The Game of Death JAVA (0) | 2022.08.26 |
| [BFS] 백준 16173 점프왕 쩰리 (Small) JAVA (0) | 2022.08.23 |